I recently graduated from Aalborg University with Master degree in Computer Science. Since then, Lars Kærlund Østergaard and I, along with our professors Jiri Srba and Kim Guldstrand Larsen published a paper on our work at SPIN 2013. Lars and I attended the conference at Stony Brook University, New York, where I presented the paper. I’ve long planned to write a series of blog posts about these things, but since I started at Mozilla I’ve been way too busy doing other interesting things. I do, however, despise the fact that my paper is hidden behind a pay-wall at Springer. So I feel compelled to use my co-author rights and release the paper here along with a few other documents, that contains proofs and results in greater detail.
- Local Model Checking of Weighted CTL (Pre-Specialization Project),
- Local Model Checking of Weighted CTL with Upper-Bound Constraints (Paper published at SPIN 2013)
- Local Model Checking of Weighted CTL with Upper-Bound Constraints (Presentation from SPIN 2013)
- On-The-Fly Model Checking of Weighed Computation Tree Logic (Specialization/Master Thesis extending the SPIN paper)
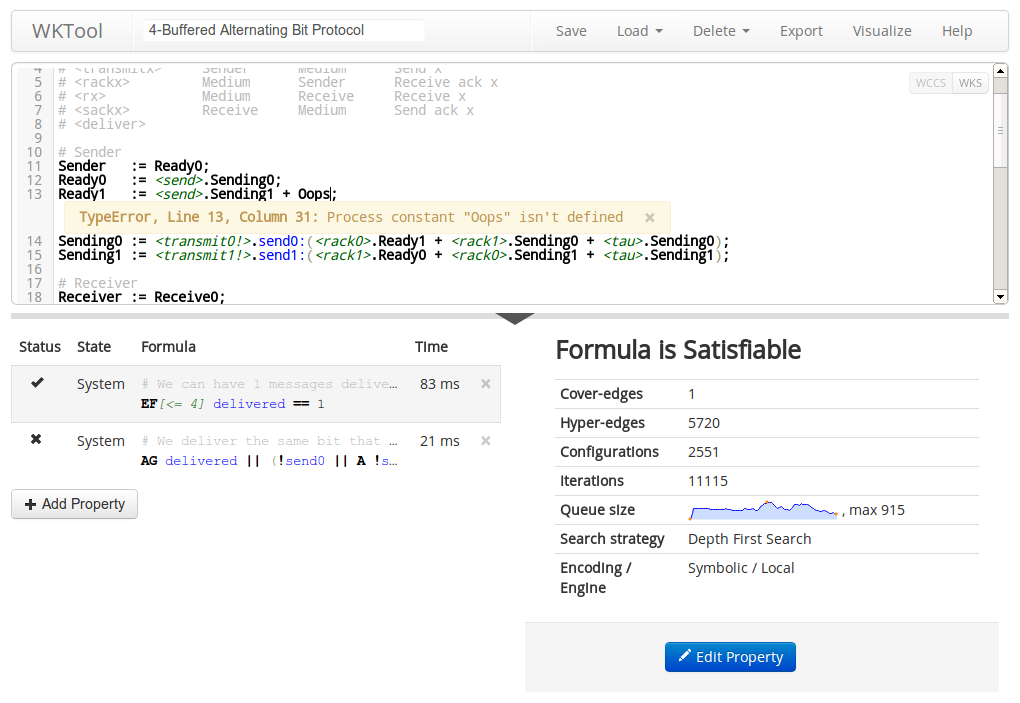
Anyways, as the headline suggests this post is mainly about model checking of Weighted Computation Tree Logic (WCTL) on Weighted Kripke Structures (WKS) in a web browser. To test out the techniques we developed for local model checking, we implemented, WKTool, a browser based model checking tool, complete with graphical user-interface, syntax highlighting, inline error messages, graphical state-space exploration, and of course on-the-fly model checking using Web Workers.
If Kripke structures and branching time logics are foreign concepts to you, this post is probably of limited interest. However, if you’re familiar with the Calculus of Communicating Systems (CCS) as used in various versions of the Concurrency Workbench, this post will give an informal introduction to the syntax of the Weighted Calculus of Communicating Systems (WCCS) and WCTL as using in WKTool.
Weighted Calculus of Communicating Systems
The following table outlines the syntax for WCCS expressions. The concepts are similar to those from Concurrency Workbench, parallel composition allows input and output actions to synchronize, and restriction forces synchronization. However, it maybe observed that actions prefixes also carry a weight. This is the weight of the transition with the action is executed, on synchronization the maximum weight is used (though this is not a technical restriction).
| Expression | Syntax |
|---|---|
| Process Definition | M := P; |
| Action Prefix | <c,8>.P or <c!,8>.P or <c>.P |
| Atomic Label | a:P |
| Parallel Composition | P | Q |
| Choice | P + Q |
| Restriction | P \ {c} or P \ {c1, c2, c3} |
| Renaming | P [a1 => a2, a3 => a4] or P [c1 -> c2, c3 -> c4] |
| Empty Process | 0 |
As WCCS defines Kripke structures and not Labelled Transistion Systems (LTS) we shall also specify atomic propositions. These are also prefixed with colon, in parallel and choice composition the atomic propositions from both sub-processes are considered. In fact, the action prefix is the only construction from which atomic propositions of the sub-process isn’t considered.
Weighted Computation Tree Logic
The full syntax of WCTL is given in the help section of WKTool, conceptually there are few surprises here. WCTL features boolean operators, atomic proposition and boolean constants as expected. However, for existential and universal until modalities, WCTL adds an optional upper-bound. For example the property E a U[<=8] b holds if there exists a path such that the atomic property a holds until the atomic property b holds, and the accumulated weight at this point does not exceed 8. Similar upper-bound is available for universal until and derived modalities.
For the existential and universal weak-until modalities WCTL offers a lower-bound constraint. For example the property E a W[>=8] b holds if there exists a path such that the atomic property a always holds, or there is a path such that the atomic property a holds until the atomic property b holds and the accumulated weight at this point isn’t less than 8. Observe that the bound has no effect if there is a path where the atomic property a always holds, thus, a zero-cycle might satisfy this property.
In the examples above the nested properties are atomic, however, WKTool does in fact support nested fixed-points when the min-max encoding us used.
Weighted On-The-Fly Model Checking with WKTool
WKTool is hosted at wktool.jonasfj.dk, you can save your models to local storage (in your browser) or export them in a JSON format that can be shared or loaded later. I’m sure most of the features are easy to locate, but do notice that under “Load” > “Load Example” the 4 last examples are the scalable models used for benchmarks in our paper. Try them out, the default scaling parameters are sane and they come with properties that can be verified, some of them even have comments to help you understand what they do.
WKTool available GNU GPLv3 and the sources are hosted at github.com/jonasfj/WKTool, it’s all in CoffeeScript using PEG.js for parsers, CodeMirror with custom lexers for highlighting, Buckets.js for data structures, Arbor.js for visualization and twitter-bootstrap for awesome styling.